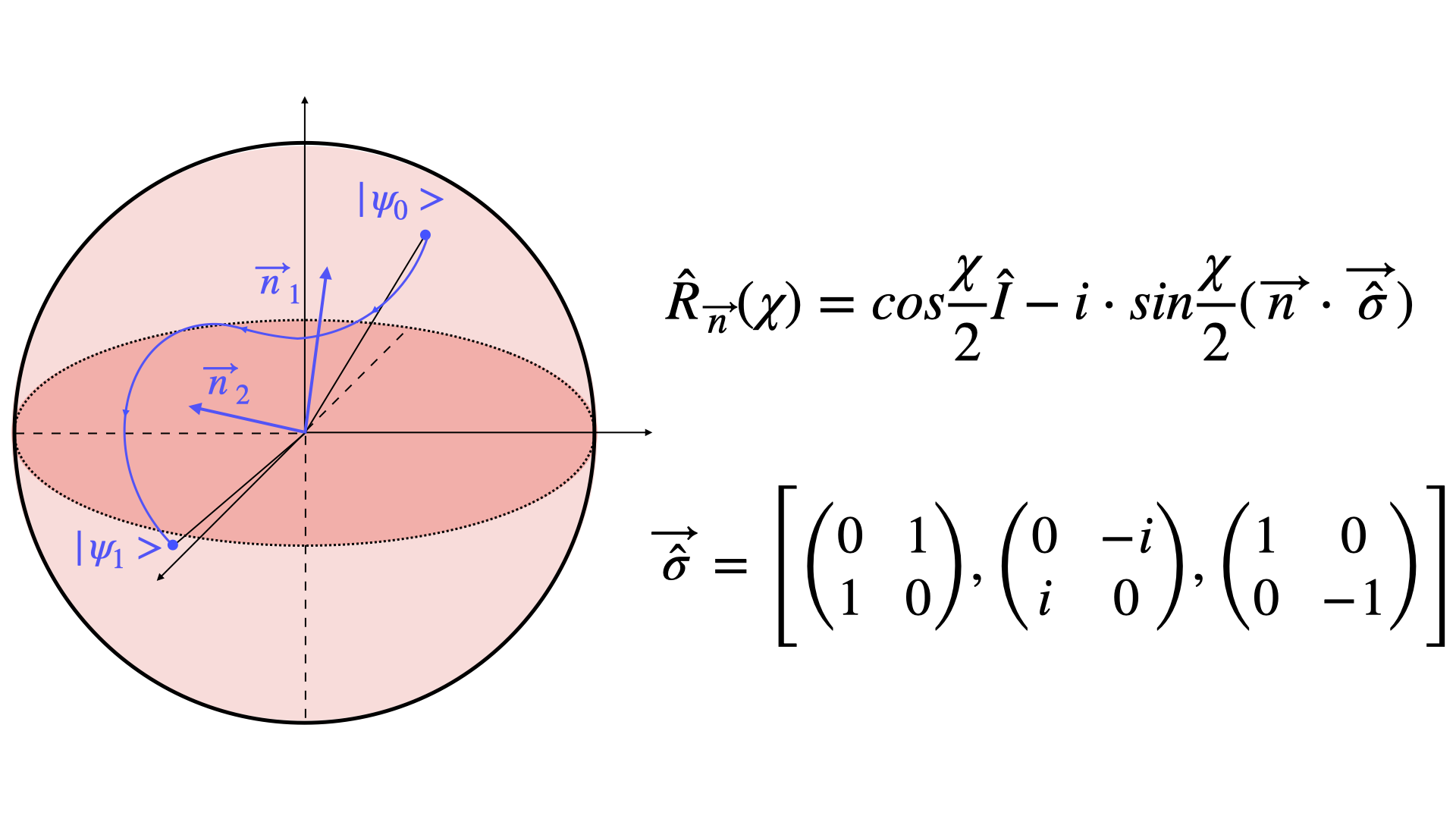Bloch sphere rotations: how to transform qubits

Pauli operators implement rotations around the corresponding axes \begin{equation} \hat{R}_x(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_x}\\ \hat{R}_y(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_y}\\ \hat{R}_z(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_z} \end{equation} while a general rotation by an angle $\chi$ around a generic axis $\vec{n}$ is given by \begin{equation} \hat{R}_{\textbf{n}}(\chi) = e^{-i\frac{\chi}{2}\textbf{n}\cdot\hat{\boldsymbol{\sigma}}} \end{equation}

Given a linear operator $\hat{O}$ such that $\hat{O}^2 = \hat{I}$, then the following equation holds \begin{equation} e^{i\theta\hat{O}} = cos\theta \hat{I} + i sin\theta \hat{O} \end{equation} PROOF Let's compute left side using the definition of exponential operator \begin{align} e^{i\theta\hat{O}} = \sum_{n=0}^{\infty} \frac{(i\theta\hat{O})^n}{n!} \\ &= \sum_{n=0}^{\infty} \frac{(i\theta\hat{O})^{2n}}{2n!} + \sum_{n=0}^{\infty} \frac{(i\theta\hat{O})^{2n+1}}{(2n+1)!}\\ &= \sum_{n=0}^{\infty} \frac{(-1)^n(\theta)^{2n}(\hat{O}^2)^n}{2n!} + i\hat{O} \sum_{n=0}^{\infty} \frac{(-1)^n(\theta)^{2n+1}(\hat{O}^2)^n}{(2n+1)!}\\ &= \text{cos}\theta \hat{I} i \text{sin}\theta \hat{O} \end{align} where we have used the fact that $\hat{O}^2 = \hat{I}$.
With this result we can no verify that the three operators written above actually perform rotations around the x, y and z axis \begin{equation} \hat{R}_x(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_x} = \text{cos}\frac{\theta}{2}\hat{I} -i \text{sin}\frac{\theta}{2}\hat{X} = \begin{pmatrix} \text{cos}\frac{\theta}{2} & - \text{i sin}\frac{\theta}{2} \\ - \text{i sin}\frac{\theta}{2} & \text{cos}\frac{\theta}{2} \end{pmatrix}\\ \hat{R}_y(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_y} = \text{cos}\frac{\theta}{2}\hat{I} -i \text{sin}\frac{\theta}{2}\hat{Y} = \begin{pmatrix} \text{cos}\frac{\theta}{2} & - \text{sin}\frac{\theta}{2} \\ \text{sin}\frac{\theta}{2} & \text{cos}\frac{\theta}{2} \end{pmatrix}\\ \hat{R}_z(\theta) = e^{-i \frac{\theta}{2}\hat{\sigma}_z} = \text{cos}\frac{\theta}{2}\hat{I} -i \text{sin}\frac{\theta}{2}\hat{Z} = \begin{pmatrix} e^{-i \frac{\theta}{2}} & 0 \\ 0 & e^{i \frac{\theta}{2}} \end{pmatrix} \end{equation} it's clear from their definition that these operators are unitary, namely $\hat{R}^{-1}_{x, y, z}(\theta) = \hat{R}^{\dagger}_{x, y, z}(\theta)$

Let's now prove that these operators actually implement rotations around the respective axes. For this, we need some preliminary results first

\begin{equation} \hat{R}(\theta)_x \longrightarrow \begin{cases} \hat{R}(\theta)_x \hat{\sigma}_x \hat{R}^{\dagger}_x = \hat{\sigma}_x\\ \hat{R}(\theta)_x \hat{\sigma}_y \hat{R}^{\dagger}_x = sin \theta \hat{\sigma}_z + cos\theta \hat{\sigma}_y\\ \hat{R}(\theta)_x \hat{\sigma}_z \hat{R}^{\dagger}_x = cos \theta \hat{\sigma}_z - sin\theta \hat{\sigma}_y \end{cases} \end{equation} \begin{equation} \hat{R}(\theta)_y \longrightarrow \begin{cases} \hat{R}(\theta)_y \hat{\sigma}_x \hat{R}^{\dagger}_y = cos \theta \hat{\sigma}_x - sin\theta \hat{\sigma}_z\\ \hat{R}(\theta)_y \hat{\sigma}_y \hat{R}^{\dagger}_y = sin \theta \hat{\sigma}_x + cos\theta \hat{\sigma}_z\\ \hat{R}(\theta)_y \hat{\sigma}_z \hat{R}^{\dagger}_y = \hat{\sigma}_z \end{cases} \end{equation} \begin{equation} \hat{R}(\theta)_z \longrightarrow \begin{cases} \hat{R}(\theta)_z \hat{\sigma}_x \hat{R}^{\dagger}_z = cos \theta \hat{\sigma}_x + sin\theta \hat{\sigma}_y\\ \hat{R}(\theta)_z \hat{\sigma}_y \hat{R}^{\dagger}_z = cos \theta \hat{\sigma}_y - sin\theta \hat{\sigma}_x\\ \hat{R}(\theta)_z \hat{\sigma}_z \hat{R}^{\dagger}_z = \hat{\sigma}_z \end{cases} \end{equation}

Suppose we have a qubit described by the density matrix \begin{equation} \hat{\rho} = \frac{1}{2} \Big[ \hat{I} + a_x \hat{\sigma}_x + a_y \hat{\sigma}_y + a_z \hat{\sigma}_z \Big] \end{equation} Let's start with $\hat{R}_x(\theta)$ \begin{align} \hat{\rho}' &= \hat{R}_x(\theta) \hat{\rho} \hat{R}^{\dagger}_x(\theta) = \frac{1}{2} \Big[ \hat{I} + a_x \hat{R}_x(\theta) \hat{\sigma}_x \hat{R}^{\dagger}_x(\theta) + a_y \hat{R}_x(\theta) \hat{\sigma}_y \hat{R}^{\dagger}_x(\theta) + a_z \hat{R}_x(\theta) \hat{\sigma}_z \hat{R}^{\dagger}_x(\theta) \Big]\\ &= \frac{1}{2} \Big[ \hat{I} + a_y(sin\theta \hat{\sigma}_z + cos\theta \hat{\sigma}_y) +a_z (cos\theta \hat{\sigma}_z - sin \theta \hat{\sigma}_y)\Big] \end{align} which corresponds to the linear transformation \begin{equation} \begin{pmatrix} a'_x \\ a'_y \\ a'_z \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & cos\theta & -sin\theta \\ 0 & sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \end{equation} this is a rotation around the $x$ axis! One can easily demonstrate that the operators $\hat{R}_y(\theta)$ and $\hat{R}_z(\theta)$ implement respectively the operators \begin{equation} \begin{pmatrix} a'_x \\ a'_y \\ a'_z \end{pmatrix} = \begin{pmatrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ -sin\theta & 0 & cos\theta \end{pmatrix} \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \hspace{1cm} \text{and} \hspace{1cm} \begin{pmatrix} a'_x \\ a'_y \\ a'_z \end{pmatrix} = \begin{pmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \end{equation} namely rotations around the $y$ and $z$ axes.

To do so, we have to perform a trick, namely we align $\vec{n}$ with the $z$ axis and then the rotation we are aiming for is just a rotation around the $z$ axis. Then we have to go back and compensate for the first rotation, namely \begin{equation} \hat{R}_{\textbf{n}}(\chi) = \hat{R}_z(\phi_{\textbf{n}})\hat{R}_y(\theta_{\textbf{n}})\hat{R}_z(\chi)\hat{R}^{-1}_y(\theta_{\textbf{n}})\hat{R}^{-1}_z(\phi_{\textbf{n}}) \end{equation} where $\phi_{\textbf{n}}$ and $\theta{\textbf{n}}$ are the angles identifying the position of $\vec{n}$ on the Bloch sphere. As said the rotation operators are Hermitian, therefore \begin{align} \hat{R}_{\textbf{n}}(\chi) &= \hat{R}_z(\phi_{\textbf{n}})\hat{R}_y(\theta_{\textbf{n}})\hat{R}_z(\chi)\hat{R}^{\dagger}_y(\theta_{\textbf{n}})\hat{R}^{\dagger}_z(\phi_{\textbf{n}})\\ &= \hat{R}_z(\phi_{\textbf{n}})\hat{R}_y(\theta_{\textbf{n}})(cos \frac{\chi}{2}\hat{I}-i sin \frac{\chi}{2}\hat{\sigma}_z)\hat{R}^{\dagger}_y(\theta_{\textbf{n}}) \hat{R}^{\dagger}_z(\phi_{\textbf{n}})\\ &= cos \frac{\chi}{2}\hat{R}_z(\phi_{\textbf{n}})\hat{R}_y(\theta_{\textbf{n}})\hat{I}\hat{R}^{\dagger}_y(\theta_{\textbf{n}})\hat{R}^{\dagger}_z(\phi_{\textbf{n}}) -i sin \frac{\chi}{2}\hat{R}_z(\phi_{\textbf{n}})\hat{R}_y(\theta_{\textbf{n}})\hat{\sigma}_z\hat{R}^{\dagger}_y(\theta_{\textbf{n}})\hat{R}^{\dagger}_z(\phi_{\textbf{n}})\\ &= cos \frac{\chi}{2}\hat{I}-i sin \frac{\chi}{2}\big(sin\theta_{\textbf{n}}cos\phi_{\textbf{n}}\hat{\sigma}_x + sin\theta_{\textbf{n}}sin\phi_{\textbf{n}}\hat{\sigma}_y + cos\theta_{\textbf{n}}\hat{\sigma}_z\big)\\ &= cos \frac{\chi}{2}\hat{I}-i sin \frac{\chi}{2}\big(n_x \hat{\sigma}_x + n_y \hat{\sigma}_y + n_z \hat{\sigma}_z\big)\\ &= cos \frac{\chi}{2}\hat{I}-i sin \frac{\chi}{2}\big(\textbf{n}\cdot\hat{\boldsymbol{\sigma}}\big) \end{align} now remembering that, for evey $\hat{O}$ such that $\hat{O}^2 = \hat{I}$ \begin{equation} e^{i\theta \hat{O}} = cos \theta \cdot \hat{I} + i sin \theta \cdot \hat{O} \end{equation} therefore we can simplify even more \begin{equation} \hat{R}_{\textbf{n}}(\chi) = e^{-i \frac{\chi}{2}\textbf{n}\cdot\hat{\boldsymbol{\sigma}}} \end{equation}