Quantum repeaters, entanglement swapping and teleportation

Direct transmission and qubit loss

In the previous example we saw how we can use use a shared entangled pair to effectively teleport a qubit between two locations, by communicating two classical bits of information. As said in the introduction, there is another way to send a qubit, which consists in literally transporting the system which encodes the qubit: we call this direct transmission. We will not focus on the technology needed for this task, but we'll just notice how this is limited by qubits loss of information, hence we can't reliably transmit over long distances without losing too much information. This means that, regardless of the method we are using, loss of informatiomn during transmission will limit our capacity tro transmit qubits.

Quantum repeaters

We saw how we basically have two ways of transmitting a qubit over a long distance: on one hand, we can teleport it, but we need to pre-share an entangled pair. Although the teleportation itself is lossless, we can't send a piece of an entangled pair arbitrarily far without losing it. On the other hand, we can send qubits directly over a channel (e.g. an optic fiber or through air) but again, the longer we go the less likely it is that the transmission will succeed. Furthermore, as we will see in the following, in the quantum world we can't simply include redundancies in our state, which is instead possible in quantum communication, and it is in fact the first protection again classical information loss. How can we overcome this issue? There are basically two ways, depending on what method of transmission we are using one-way quantum repeaters for direct transmission, and symmetric repeaters for teleportation.

Symmetric quantum repeaters and entanglement swapping

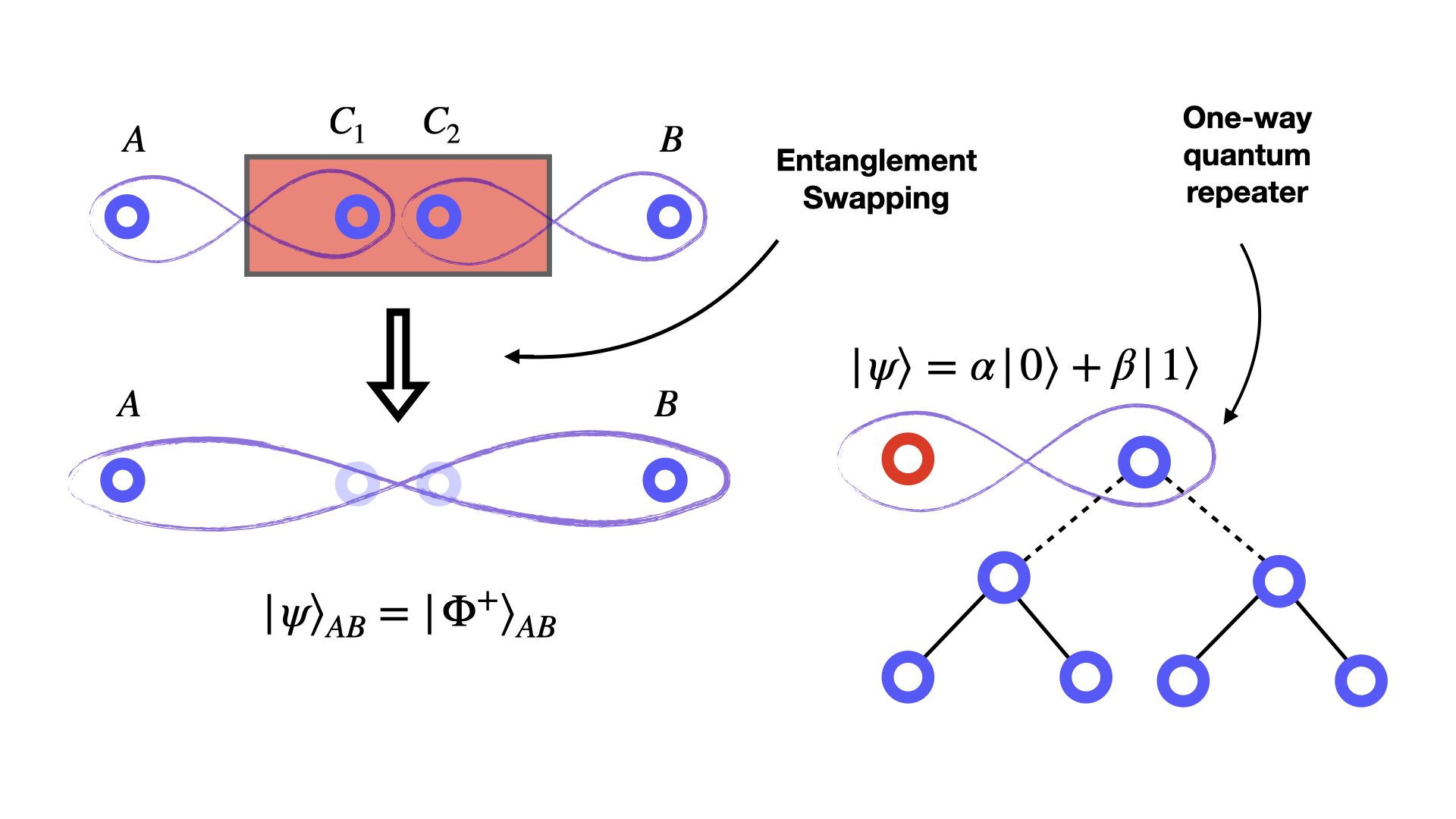
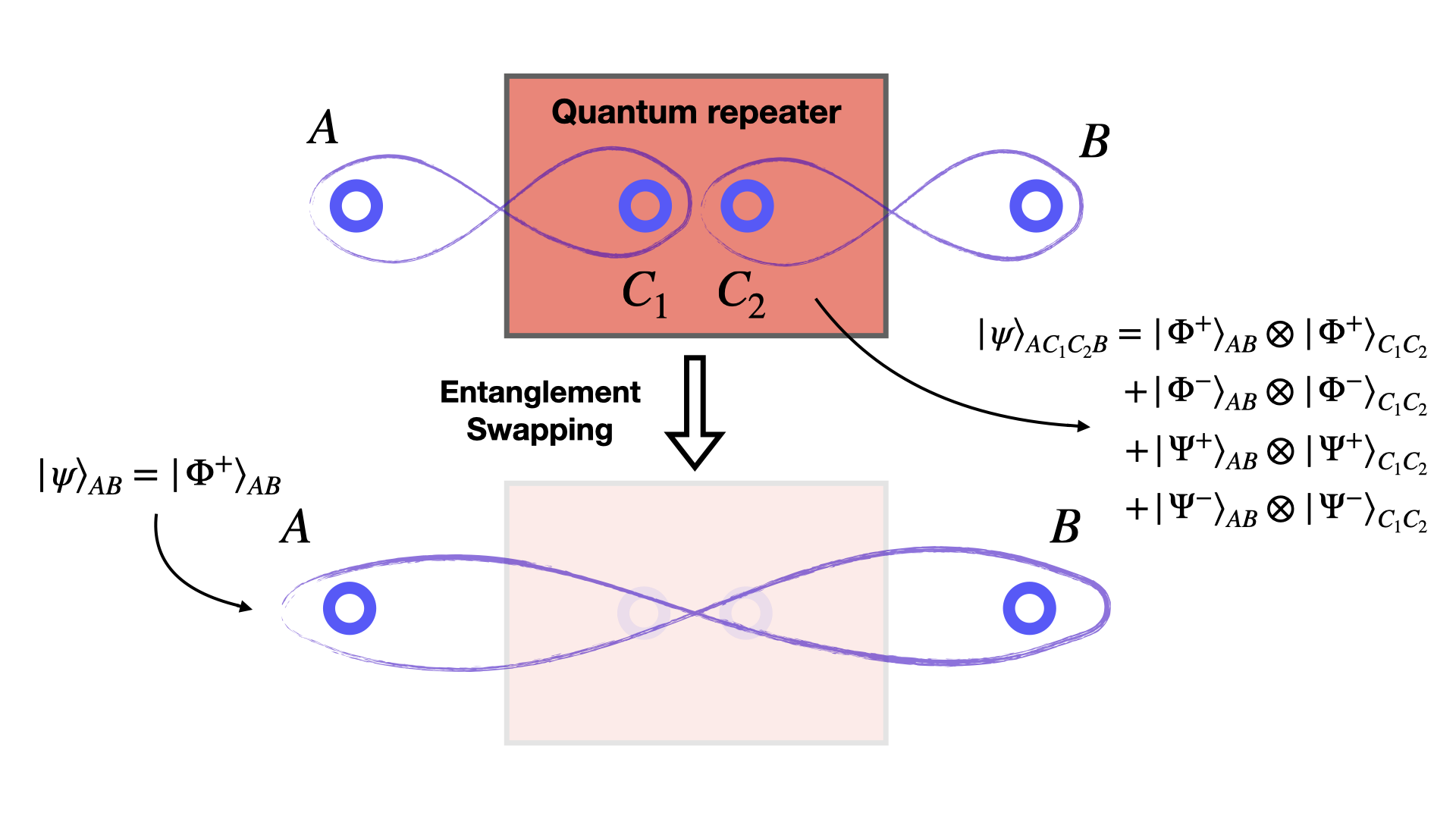
The first type of repeater is used to increase the distance of the teleportation protocol. In a nutshell, the limiting factor of this protocol is the impossibility to generate entanglement between two very distant locations $A$ and $B$. The solution to this issue, is what's called entanglement swapping, which, rouhgly speaking, lets us generate a chain of entangled states, that can be then joined to obtain an entangled state between possibly very far points.

Entanglement swapping

Let's see how this works. Suppose we have three locations, $A$, $B$ and $C$, where $C$ is exactly in the middle and it's the "repeater location": $A$ and $B$ will have one qubit each, while $C$ will have two qubits, let's call them $C_1$ and $C_2$ and suppose our technology only permits to reliably share an entangled couple between $A$ and $C$, or $C$ and $B$, but it's not enough to share an entangled pair between $A$ and $B$ directly. What we can do, is share two entangled pairs, between $A$ and $C$, and between $C$ and $B$, suppose for simplicity that we are using the same Bell states we used for teleportation, namely $|\Phi^+\rangle_{AC_ 1}$ and $|\Phi^+\rangle_{C_2B}$

One-way quantum repeaters

In the previous section we saw how we can use entanglement swapping to build a chain of entangled states ad then join them by creating a very long entangled state that we can use for teleportation: this way, once we will have quantum memories, we'll be able to perform teleportation actross arbitrary distances. Let's now see how we can use another kind of repeaters to enhance direct transmission as well.

The no-cloning theorem

At first, we would be tempted to simply copy our qubit $N$ times, and send them all together, just like we do in classical communications. This way, we would just need intermediate stations that could amplify our signal, namely copy our qubits, and send them to the next station. Although this sounds like the natural way to go, physics doesn't allow this method, and the reason is that, in the quantum world, we can't copy a state without destroying it, which means we can't copy it at all. This is assured by the no cloning theorem So it's impossible to build the quantum counterpart of a repeater, so how do we do that? It turns out that, again, we can use entanglement.

Teleportation protocol

As weird as it sounds, instead of physically transmitting a qubit, we can teleport it. This is because a qubit is completely defined by the two parameters $\alpha$ and $\beta$, so if we manage to obtain the another qubit in a different place, having the same exact parameters, we can say we have teleported it. The main resource that let's us do this is entanglement.

Entanglement

Simply said, an entangled quantum state is a state, made of at least two sub-systems $A$ and $B$, that is such that each of the systems can't be described independently from the other. In other words, if we only look at one of them, we'll see properties that we can't explain if we don't take the other system into account. On the other hand, a system that can be seen as the sum of its parts, and such that each part acts independently, is said to be separable. A state of this kind can always be written as $$ |\psi\rangle = |\phi_A\rangle \otimes |\phi_B\rangle $$ where the $\otimes$ symbols represents the "tensor product" and it captures the idea of independent systems, which are just attached together but remain two separate entities. On the other hand, it's impossible to write an entangled state in such a way, for example $$ |\Phi^+\rangle_{AB} = \frac{| 0 \rangle \otimes |0\rangle + |1\rangle \otimes |1 \rangle}{\sqrt{2}} $$ is called a Bell state, and there is no way we'll be able to write as the tensor product of two different states. A fascinating property of entangled states, which is a direct consequence of the collapse of the wave function postulate, is that we can prepare an entangled state in some location, and then send a part of this system in a location $A$, and another part in a location $B$ (for example we can entangle two photons in a lab in Rome, and then send one of the photons through an optic fiber to Paris). At this point, one can make a measurement in one of the locations, and we are assured, that even though they can be at an incredibly large distance, we can predict with $100\%$ accuracy the result of the other measurement at the other location. Let's see an example: Let's take the Bell state again, and suppose we are sending one qubit at the location $A$ and the other at the location $B$, then we'll write this state as $$ |\Phi^+\rangle_{AB} = \frac{| 0 \rangle_A \otimes |0\rangle_B + |1\rangle_A \otimes |1 \rangle_B}{\sqrt{2}} $$ suppose we measure the qubit in $A$, and we find $|0\rangle_A$ (for example we let the photon through a polarizer and we find it to be polarized horizontally. We can use the encoding $| H \rangle \rightarrow | 0 \rangle$ and $| V \rangle \rightarrow | 1 \rangle$). Now the wave function of the whole system has collapsed as a result of our measurement, so the whole system is now in the state $|\psi\rangle = |0\rangle_A\otimes |0\rangle_B$, but what does it mean? It means that if the qubit in $B$ is now measured we will find $|0\rangle_B$ without doubt, so the measurement in $A$ affected the measurement in $B$ regardless of their distance, and this happens instantaneously! Although we could prove that we can't use this property to send information faster than light (violating special relativity), we can use it as a resource to teleport a qubit.

Teleportation protocol

Let's now delve into how we can effectively transmit qubits. The protocol is pretty simple, and it goes like this:

1) First of all, the two parties, let's call them Alice and Bob, share an entangled system, for example a third person, Carl, could prepare the Bell state $$ |\Phi^+\rangle = \frac{| 0 \rangle_A \otimes |1\rangle_B + |1\rangle_A \otimes |1 \rangle_B}{\sqrt{2}} $$ and send one qubit to Alice, and one qubit to Bob. Now we know, that regardless of their system, if one of them performs a measurement, the other one will measure the same qubit, with $100\%$ probability.

2) Let's say that now Alice wants to send the qubit $$ |\psi\rangle_O = \alpha |0\rangle_O + \beta |1\rangle_O $$ she would like to somehow exploit the entangled state that she shares with Bob, so she has to somehow "entangle" her first qubit $|\psi\rangle_O$ to her second qubit ($A$), and then do something on it such that Bob can "feel" what happened by performing a measurement on his qubit: remember that they share an entangled state, and there is a $100\%$ correlation between their measuremets. To do so, Alice will have to entangle her two qubits, and to see how she can do it, let's first rewrite the whole system state in a more convenient way $$ |\psi\rangle_{OAB} = \big(\alpha |0\rangle_O + \beta |1\rangle_O\big) \otimes\Bigg( \frac{| 0 \rangle_A \otimes |1\rangle_B + |1\rangle_A \otimes |1 \rangle_B}{\sqrt{2}}\Bigg) $$ Before continuing, let's define the four Bell states, which form a basis for $\mathbb{C}^4$ made of entangled states $$ \begin{cases} |\Phi^+\rangle \equiv \frac{|0\rangle \otimes |0\rangle + |1\rangle \otimes |1\rangle}{\sqrt{2}}\\ |\Phi^-\rangle \equiv \frac{|0\rangle \otimes |0\rangle - |1\rangle \otimes |1\rangle}{\sqrt{2}}\\ |\Psi^+\rangle \equiv \frac{|0\rangle \otimes |1\rangle + |1\rangle \otimes |0\rangle}{\sqrt{2}}\\ |\Psi^-\rangle \equiv \frac{|0\rangle \otimes |1\rangle - |1\rangle \otimes |0\rangle}{\sqrt{2}} \end{cases} $$ By simply expanding and collecting in a different way, it's easy to show that the overall state can be re-written conveniently as $$ |\psi\rangle_{OAB} = \frac{1}{2}\Big[|\Phi^+\rangle_{OA}\otimes(\alpha |0\rangle_B+\beta|1\rangle_B)+|\Phi^-\rangle_{OA}\otimes(\alpha |0\rangle_B-\beta|1\rangle_B)+|\Psi^+\rangle_{OA}\otimes(\alpha |1\rangle_B+\beta|0\rangle_B)+|\Psi^-\rangle_{OA}\otimes(\alpha |1\rangle_B-\beta|0\rangle_B)\Big] $$

3) Let's take a look at what we have: we managed to re-write the overall system as a sum, where each term is the tensor product of two pieces, the first piece is a 2-qubit state, all posessed by Alice, the second one is a single qubit, all posessed by Bob, which could be manipulated to recover the initial qubit (we'll see how in a moment). Suppose now Alice performs a Bell measurement on her two qubits, this can be done in a standard way with a suitable quantum circuit, and we could prove that when making this measurement, we have a $25\%$ chance of getting one of the four Bell states. For each of the outcomes, the whole quantum state will collapse, so we end up in one of four equally probable situations

• Alice measures $|\Psi^+\rangle$, then Bob has $\alpha|0\rangle+\beta|1\rangle$
• Alice measures $|\Psi^+\rangle$, then Bob has $\alpha|0\rangle-\beta|1\rangle$
• Alice measures $|\Phi^+\rangle$, then Bob has $\alpha|1\rangle+\beta|0\rangle$
• Alice measures $|\Phi^-\rangle$, then Bob has $\alpha|1\rangle-\beta|0\rangle$

In each of these cases it's easy for Bob to recover his initial qubit, in particular he only needs one of the four transformations in the Pauli group to recover it. To see this, let's express the qubits as column vectors in the computational basis $\{|0\rangle,|1\rangle\}$. This lets us represent a qubit $|\psi\rangle = \alpha|0\rangle +\beta |1\rangle$ like $$ \psi = \begin{pmatrix}\alpha\\ \beta\end{pmatrix} $$ let's rewrite Bob's state, after Alice's measurement, in this notation

• Alice measures $|\Psi^+\rangle$, then Bob has $\begin{pmatrix}\alpha\\ \beta\end{pmatrix}$
• Alice measures $|\Psi^-\rangle$, then Bob has $\begin{pmatrix}\alpha\\ -\beta\end{pmatrix}$
• Alice measures $|\Phi^+\rangle$, then Bob has $\begin{pmatrix}\beta\\ \alpha\end{pmatrix}$
• Alice measures $|\Phi^-\rangle$, then Bob has $\begin{pmatrix}\beta\\ -\alpha\end{pmatrix}$

It is simple to verify that, in order for Bob to get the initial qubit $\psi = \begin{pmatrix}\alpha\\ \beta\end{pmatrix}$, he will have to perform one of the four operations $$ \begin{cases} \begin{pmatrix}\alpha\\ \beta\end{pmatrix} = \begin{pmatrix}1&0\\0&1\end{pmatrix}\begin{pmatrix}\alpha\\ \beta\end{pmatrix} = \hat{I}\begin{pmatrix}\alpha\\ \beta\end{pmatrix}\\ \begin{pmatrix}\alpha\\ \beta\end{pmatrix} = \begin{pmatrix}1&0\\0&-1\end{pmatrix}\begin{pmatrix}\alpha\\ -\beta\end{pmatrix} = \hat{\sigma}_z \begin{pmatrix}\alpha\\ -\beta\end{pmatrix}\\ \begin{pmatrix}\alpha\\ \beta\end{pmatrix} = \begin{pmatrix}0&1\\1&0\end{pmatrix}\begin{pmatrix}\beta\\ \alpha\end{pmatrix} = \hat{\sigma}_x \begin{pmatrix}\beta\\ \alpha\end{pmatrix}\\ \begin{pmatrix}\alpha\\ \beta\end{pmatrix} = \begin{pmatrix}0&-i\\i&0\end{pmatrix}\begin{pmatrix}\beta\\ -\alpha\end{pmatrix} = \hat{\sigma}_y \begin{pmatrix}\beta\\ -\alpha\end{pmatrix} \end{cases} $$

4) Bob could operate a simple transformation on his state to simply recover the initial qubit, but how does he know which one? Simple, Alice knows which of the four Bell states she got, so she only needs to tell Bob. Since there are $4$ possibilities, she only needs to send him $2$ (classical) bits of information to tell him which of the four states he got, then he will know which operation to perform without the need to measure his qubit, which would destroy it. In the end, Alice and Bob managed to teleport one qubit by exploiting a shared entangled state and the classical communication of two bits. Although this seems like a magical procedure, keep in mind that the distance we can transmit is limited by the distance one is able to share the entangled pair, which is however limited.

After this operation is performed, the overall state will be the following $$ |\psi\rangle_{AC_1C_2B} = |\Phi^+\rangle_{AC_1}\otimes |\Phi^+\rangle_{C_2B} = \frac{1}{2}\Bigg[|0000\rangle_{AC_1C_2B}+|0011\rangle_{AC_1C_2B}+|1100\rangle_{AC_1C_2B}+|1111\rangle_{AC_1C_2B}\Bigg] $$ it's easy to verify, that we can rearrange the terms in the following way $$ |\psi\rangle_{AC_1C_2B} = |\Phi^+\rangle_{AB}\otimes |\Phi^+\rangle_{C_1C_2} + |\Phi^-\rangle_{AB}\otimes |\Phi^-\rangle_{C_1C_2} + |\Psi^+\rangle_{AB}\otimes |\Psi^+\rangle_{C_1C_2}+|\Psi^-\rangle_{AB}\otimes |\Psi^-\rangle_{C_1C_2} $$ Now we can perform a Bell measurement at the repeater site $C$ and by doing so, we can end up in one of the four Bell states $\{|\Phi^+\rangle_{C_1C_2}, |\Phi^-\rangle_{C_1C_2}, |\Psi^+\rangle_{C_1C_2}, |\Psi^-\rangle_{C_1C_2}\}$, but what's important, is that regardless of the result, the state between $A$ and $B$ will be a Bell state as well, namely an entangled state! Now, if $C$ communicates to $B$ which state he got, $B$ will be able to perform one of four simple operations (we could show these operations to be very similar to the ones needed in the teleportation protocol) to transform his state into $|\Phi^+\rangle_{AB}$. At the end of this procedure, we'll have successfully extended an entangled state between $A$ and $B$ by using a chain of two entangled states, using an intermediate repeater. It's easy to convince ourselves that we can do this any number of times using a chain of entangled states as long as we need.

Quantum memories

There is a critical factor that we didn't mention while explaining the entanglement swapping procedure, and this is that, in order to perform this operation, we need to conserve two different entangled states, before joining them together by performing a Bell measurement and this requires what's known as quantum memories. Although a lot of research is being carried out, there is no current implementation capable of maintaining a quantum system's coherence for a long enogh time, which makes this protocol not applicable with the current technology.

We are not going to delve into the details, which would require too much time and knowledge, but we can get the basic idea from a clarifying example. Suppose we are trying to send a qubit $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ but we know we are going to lose it with some non-negligible probability, which will approach $100\%$ as the transmission distance increases. What we can try to do, is creating entanglement between this qubit and other qubits, in a way that will "spread" the information of the qubit we are trying to transmit across the whole state, in such a highly correlated way that, in case some qubits are lost, we'll be able to still recover the initial qubit. If we manage to do so, it will be sufficient to have intermediate stations that deconde the received state, prepare the new entangled states and send them to the next station. It turns out that this is indeed possible, and the way we can do this in practice is to entangle our qubit to a quantum graph state (check out this article on quantum graph states). Instead of the general theory, let's see one example. Suppose we want to transmit the qubit $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ and we have a device that is capable of generating the following tree state $$ |G\rangle = \frac{1}{2^{\frac{3}{2}}}\Big[|0\rangle (|0\rangle|++\rangle+|1\rangle|--\rangle)^{\otimes 2}+|1\rangle (|0\rangle|++\rangle-|1\rangle|--\rangle)^{\otimes 2}\Big] $$ by expanding the state (it's very long, it has $2^7 = 128$ terms!) we could use a simple algorithm to check that this is exactly the tree represented in the first part of the figure below.

Notice how we can divide the three state in layers, the root, branches and leaves layers, and how each qubit of these layers can be represented in an ordered way in the quantum state that this tree graph is representing. Now let's see how the procedure works in practice, by breaking it down intro three parts:

Encoding First of all, we have to generate entanglement between our qubit and our tree state. To do so, we have seen throughout this article that the simplest way is performing a Bell measurement between the qubits we are trying to entangle, in this case between the qubit we are encoding ($\alpha |0\rangle +\beta |1\rangle$) and the root of the tree state $$ |G\rangle \equiv \frac{1}{2^{\frac{3}{2}}}\Big[|0\rangle_R (|0\rangle_B|++\rangle_L+|1\rangle_B|--\rangle_L)^{\otimes 2}+|1\rangle_R (|0\rangle_B|++\rangle_L-|1\rangle_B|--\rangle_L)^{\otimes 2}\Big] $$ after performing the Bell measurement, we can discard the root qubit and we are left with $$ \frac{\alpha}{2}(|0\rangle_B|++\rangle_L+|1\rangle_B|--\rangle_L)^{\otimes 2}+ \frac{\beta}{2} (|0\rangle_B|++\rangle_L-|1\rangle_B|--\rangle_L)^{\otimes 2} $$

Qubit loss Now suppose to transmit the resulting state, and suppose to lose one branch qubit and two leaves qubits (represented in the figure). This is a realistic example, where we have a substantial probability of losing each qubit during transmission. The quantum state, once these qubits have been lost, is transformed to the mixed state $$ \begin{cases} \frac{1}{\sqrt{2}}|+\rangle_L\big[(\alpha+\beta)|0\rangle_B |++\rangle_L+(\alpha-\beta)|1\rangle_B|--\rangle_L\big]\\ \frac{1}{\sqrt{2}}|-\rangle_L\big[(\alpha-\beta)|0\rangle_B |++\rangle_L+(\alpha+\beta)|1\rangle_B|--\rangle_L\big] \end{cases} $$ were the two outcomes have $50/50$ probability.

Decoding Suppose we received the incomplete quantum state and we would like to recover the two parameters $\alpha,\beta \in \mathbb{C}$, this would mean recover the qubit we were trying to transmit. The procedure we can use is the following:

1) First of all, we can perform an $x$ measurement on the first qubit, which can reveal the state $|+\rangle$ or $|-\rangle$: this way, we have found which state we are in.

2) Suppose we found $|+\rangle$, then the state we are left with is $$ \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B (| 00\rangle_L+| 01\rangle_L+| 10\rangle_L+| 11\rangle_L)+(\alpha-\beta)| 1\rangle_B (| 00\rangle_L-| 01\rangle_L-| 10\rangle_L+| 11\rangle_)\big] $$ which can be conveniently rearranged as $$ \begin{align} \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B + (\alpha-\beta)| 1 \rangle_B\big]| 00 \rangle_L\\ \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B - (\alpha-\beta)| 1 \rangle_B\big]| 01 \rangle_L +\\ \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B - (\alpha-\beta)| 1 \rangle_B\big]| 10 \rangle_L +\\ \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B + (\alpha-\beta)| 1 \rangle_B\big]| 11 \rangle_L \end{align} $$ Now we can measure the last two qubits in the $z$ basis, having one of four possible outcomes. Suppose our $z$ measurements reveals the state $|00\rangle_L$, then we are left with the state $$ \frac{1}{\sqrt{2}}\big[(\alpha+\beta)| 0 \rangle_B + (\alpha-\beta)| 1 \rangle_B\big] = \alpha | + \rangle_B +\beta | - \rangle_B $$

3) At this point, it is sufficient to apply an Hadamard gate to our qubit to recover $\alpha |0\rangle + \beta |1\rangle$. We could show that, for any other combination, we could come up with a corresponding (simple) operation to perform to recover our qubit.

Although we showed this procedure for one particular case, we could show there is a whole class of possible situations where, by encoding our qubit this way, we are able to recover the initial parameters, even after a substantial percentage of the qubits has been lost. In other words, we managed to transmit a qubit over a noisy channel, and recover it even after information loss, without breaking the no cloning theorem.

Qubit transmission and teleportation protocol

Quantum communication is the branch of physics and engineering that deals with the transmission of quantum information throught communication channels. In theory, every system that has some amount of quantum coherence will be suitable to encode and transmit quantum information. In this article, we will focus on a widely studied form of quantum information, the qubit (take a look at this article to know more about qubits). In the same way a bit is the smallest digital piece of information, a qubits is the smalles quantum piece of information. In particular, a qubit is a quantum system which can be represented by a 2 dimensional complex vector $$ | \psi \rangle = \alpha | 0 \rangle + \beta | 1\rangle $$ where $\alpha, \beta \in \mathbb{C}$. How can we send such qubit from one location to the other, without destroying it? There are basically two ways: we can send it as is (e.g. sending a photon through an optic fiber) or we can teleport it! Both ways lose their strength as the distance of transmission is increased, and that's why we need quantum repeaters: a quantum repeater is a device that let's us increase the distance we can transmit a qubit (just like a normal repeater does with a radio signal, for example). Roughly speaking, there are two kinds of repeaters: symmetric quantum repeaters, which enable quantum teleportation across long distances through entanglement swapping, and one-way quantum repeaters, whichh enhance direct transmission, by encoding qubits in highly entangled graph states. In the following section, we're going to focus on the teleportation method.

Conclusions

In this article, we have seen how a qubit can be basically transmitted in two ways: by direct transmission and through quantum teleportation. In both cases, the distance a quantum system can be reliably transmitted without loss of coherence is the limiting factor, and in both cases we need devices that let us increase this distance. On one hand, we can exploit symmetric quantum repeaters that, once quantum memories will be available, will let us extend, through enanglement swapping, an entangled pair between any two locations. On the other hand, one-way quantum repeaters let us overcome the no cloning theorem, and encode a qubit into a highly entangled graph state, that can be used to encode the qubit and protect it from information loss during transmission.

Bibliography

[1] Nielsen, M.A. and Chuang, I., 2002. Quantum computation and quantum information.
[2] Borregaard, J., Pichler, H., Schröder, T., Lukin, M.D., Lodahl, P. and Sørensen, A.S., 2020. One-way quantum repeater based on near-deterministic photon-emitter interfaces. Physical Review X, 10(2), p.021071.